|
|
giải đáp
|
hình học không gian
|
|
|
|
Trong mp(SAC) kẻ AC' vuông góc với SC (1)
Trong mp(SAB) kẻ AB' vuông góc với SB. Lại có: BC vuông góc với (SAB)
=> AB' vuông góc với (SBC) => AB' vuông góc với SC (2)
Trong mp(SAD) kẻ AD' vuông góc với SD. Lại có: DC vuông góc với (SAD)
=> AD' vuông góc với (SDC) => AD' vuông góc với SC (3)
(1)(2)(3) => SC vuông góc với mp(AB'C'D'). Như vậy mp(AB'C'D') chính là thiết diện ($\alpha$) cần tìm.
Ta có: $\Delta$SB'A = $\Delta$SD'A (g.c.g) => AB'= AD' (4)
Lại có: $\Delta$SC'B' = $\Delta$SC'D' (c.g.c) => C'B'= C'D' (5)
(4)(5)=> $\Delta$AB'C' = $\Delta$AD'C'
=> 2 đường chéo của tứ giác AB'C'D' vuông góc với nhau
=> $S_{AB'C'D'}$ = 1/2. AC'. B'D'
Có: AC' là đường cao trong $\Delta$SAC vuông tai A => $\frac{1}{AC'^{2}}$= $\frac{1}{AS^{2}}+\frac{1}{AC^{2}}$ => AC'= a. $\sqrt{\frac{2}{3}}$
Lại có: AB' là đường cao trong $\Delta$SAB vuông tai A => $\frac{1}{AB'^{2}}$= $\frac{1}{AS^{2}}+\frac{1}{AB^{2}}$ => AB'= $\frac{a}{\sqrt{2}}$
$\Delta$SB'A vuông tai B' => SB'= $\frac{a}{\sqrt{2}}$
Có: SB=SD, SB'=SD' => $\frac{SB'}{SB}$= $\frac{SD'}{SD}$ => $\Delta$SB'D' đồng dạng với $\Delta$SBD
=> B'D'/BD= SB'/SB= $\frac{\frac{a}{\sqrt{2}}}{a\sqrt{2}}$= 1/2 => B'D' = $\frac{a\sqrt{2}}{2}$
Như vậy: $S_{AB'C'D'}$ = 1/2. a. $\sqrt{\frac{2}{3}}$. $\frac{a\sqrt{2}}{2}$ = $\frac{a^{2}}{2\sqrt{3}}$
|
|
|
|
giải đáp
|
những bài toán quen mà lạ
|
|
|
|
BC=a, AC=b, AB= c
Có: $\begin{cases}b^{2}= c^{2}+a^{2}- 2ca. cosB \\ c^{2}= a^{2}+ b^{2}- 2ab. cosC \end{cases}$
=> $\begin{cases}b^{2}- c^{2}= 121- 22c. cos35 (1)\\ c^{2}- b^{2}= 121- 22b. cos70 (2) \end{cases}$
=> 11- 2c.cos35= 2b. cos70- 11
=> 11= b. cos70+ c. cos35 (3)
Thế (3) vào (1) hoặc (2) để giải tiếp nhé :)
|
|
|
|
giải đáp
|
Nhị thức Newton.
|
|
|
|
Khai triển nhị thức Newton: $(1+x+x^{2}+x^{3})^{15}$
= $C^{k}_{15}$. $(x+x^{2}+x^{3})^{k}$
= $C^{k}_{15}$. $C^{t}_{k}$. $x^{k-t}$ $(x^{2}+x^{3})^{t}$
= $C^{k}_{15}$. $C^{t}_{k}$. $x^{k-t}$. $C^{m}_{t}$ $(x^{})^{2m}$. $x^{3.(t-m)}$
= $C^{k}_{15}$. $C^{t}_{k}$. $C^{m}_{t}$. $x^{k+2t-m}$
Khi đó ta cần tìm (k,t,m) sao cho: k+2t-m=0, k$\leqslant $ 15, t$\leqslant $k, m$\leqslant $t
=> (k,t,m)= $\left\{ {(4,3,0),(4,4,2),(5,3,1),(5,4,3),(5,5,5),(6,2,0),(6,3,2),(6,4,4),(7,2,1),(7,3,3),(8,1,0),(8,2,2),(9,1,1),(10,0,0)} \right\}$
Vậy hệ số của $x^{10}$ trong khai triển là: 1392456
|
|
|
|
giải đáp
|
Hình không gian
|
|
|
|
Đồng nhất hình vẽ với hệ tọa độ trong không gian sao cho A' là gốc tọa độ, A'B; trùng Ox, A'D' trùng Oy, A'A trùng Oz
Khi đó, A'(0,0,0), M(1/2,0,0), N(1,1/2,1), P(0,1,1/2), A(0,0,1), C'(1,1,0)
Ta có: $\overrightarrow{AC}$= (1,1,-1)
$\overrightarrow{MN}$= (1/2,1/2,1)= (1,1,2)
$\overrightarrow{MP}$= (-1/2,1,1/2)= (-1,2,1)
=> Vector pháp tuyến $\overrightarrow{n}$ của mp(MNP) là: $\left[ {\overrightarrow{MN},\overrightarrow{MP}} \right]$= (-3,-3,3)
Ta thấy tọa độ của $\overrightarrow{n}$ tỉ lệ với tọa độ của $\overrightarrow{AC}$ => AC' vuông góc với mp(MNP) -đpcm
|
|
|
|
sửa đổi
|
Hàm số đồ thị HELPPPPPPPPP .. mình cần rất gấp ... ai có thể giúp mình nào ... :((
|
|
|
|
a/ $\overrightarrow{AB}$=(2-m, m-4) => AB= $\sqrt{(2-m)^{2}+(m-4)^{2}}$ =$\sqrt{2m^{2}-12m+20}$= $\sqrt{2.((m-3)^{2}+1)}$ nhỏ nhất $\Leftrightarrow $ m=3b/ Giả sử các điểm thỏa mãn là (x, y)=> (x,y)= $\left\{ {x,y \in } Z^{+}, 3x+4y=21\right\}$ =$\left\{ {(3,3),(7,0)} \right\}$
a/ $\overrightarrow{AB}$=(2-m, m-4) => AB= $\sqrt{(2-m)^{2}+(m-4)^{2}}$ =$\sqrt{2m^{2}-12m+20}$= $\sqrt{2.((m-3)^{2}+1)}$ nhỏ nhất $\Leftrightarrow $ m=3b/ Giả sử các điểm thỏa mãn là (x, y)=> (x,y)= $\left\{ {x,y \in } Z^{+}, 3x+4y=21\right\}$ =$\left\{ {(3,3),(7,0)} \right\}$c/ Hai đường thẳng: 2k.x+ (k-1).y=2 và $\sqrt{3}$.x-y=0$\Leftrightarrow $ $\frac{2k}{\sqrt{3}}$=$\frac{k-1}{-1}$ => k= $\frac{\sqrt{3}}{\sqrt{3}+2}$
|
|
|
|
|
|
giải đáp
|
Một bạn trên facebook hỏi
|
|
|
|
Áp dụng công thức: 1+ $(tan(x))^{2}$= $\frac{1}{(cos(x))^{2}}$ với x$\neq $$\Pi/2$+k$\Pi$ (k$\in $Z)
Có: tan x= 3/2 => $(cos(x))^{2}$= 4/13 => cos x= $\pm $$\sqrt{4/13}$
Có: tan x= $\frac{sin x}{cos x}$= 3/2 => sin x= $\frac{3}{2}$. ($\pm $$\sqrt{\frac{4}{13}}$)
Có: 1+ $(cot(x))^{2}$= $\frac{1}{(sin(x))^{2}}$ với x$\neq $k$\Pi$ (k$\in $Z) => $(cot(x))^{2}$= $\frac{4}{9}$ => cot x= $\pm \frac{2}{3}$
|
|
|
|
bình luận
|
các phép toán trên tập hợp
Đây là lời giải theo suy nghĩ logic của mình, đây là 1 bài logic hay 1 bài đơn thuần toán và phải trả lời theo ngôn ngữ toán hả bạn!
|
|
|
|
|
|
|
|
sửa đổi
|
các phép toán trên tập hợp
|
|
|
|
Coi bài phải là làn hững bài phải nộpK\B= $\left\{ {bài tập chưa làm trong sách} \right\}$K\A= $\left\{ {bài tập trong sách nhưng không nhất thiết phải làm} \right\}$B\A= $\left\{ {bài tập đã làm nhưng không phải nộp} \right\}$A\B= $\left\{ {bài tập cần nộp nhưng chưa làm} \right\}$A$\cap $B= $\left\{ {bài tập phải nộp và đã làm} \right\}$
Coi bài phải là làn hững bài phải nộpK\B= $\left\{ {bài tập chưa làm trong sách} \right\}$K\A= $\left\{ {bài tập trong sách nhưng không nhất thiết phải làm} \right\}$B\A= $\left\{ {bài tập đã làm nhưng không phải nộp} \right\}$A\B= $\left\{ {bài tập cần nộp nhưng chưa làm} \right\}$A$\cap $B= $\left\{ {bài tập phải nộp và đã làm} \right\}$
|
|
|
|
giải đáp
|
các phép toán trên tập hợp
|
|
|
|
Coi bài phải là làn hững bài phải nộp
K\B= $\left\{ {bài tập chưa làm trong sách} \right\}$
K\A= $\left\{ {bài tập trong sách nhưng không nhất thiết phải làm} \right\}$
B\A= $\left\{ {bài tập đã làm nhưng không phải nộp} \right\}$
A\B= $\left\{ {bài tập cần nộp nhưng chưa làm} \right\}$
A$\cap $B= $\left\{ {bài tập phải nộp và đã làm} \right\}$
|
|
|
|
bình luận
|
hình hoc không gian
Gỉa sử ngược lại SC vuông góc với (BHK)=> SC vuông góc với BK. Mà K là trọng tâm của tam giác SBC => SC không thể vuông góc với BK (mâu thuẩn với điều giả sửSC vuông góc vs BK khi SBC cân (gt này đề bài không cho)=> đề bài sai!
|
|
|
|
|
|
|
|
sửa đổi
|
hình hoc không gian
|
|
|
|
a/ +)K là trọng tâm $\Delta$ SBC => SC vuông góc với BKH là trọng tâm $\Delta$ ABC=> BH vuông góc với SC=> SC vuông góc với (BHK)+) SC vuông góc với BKSA vuông góc với BH=> (SAC) vuông góc với (BHK)
a/ +)K là trực tâm $\Delta$ SBC => SC vuông góc với BKH là trực tâm $\Delta$ ABC=> BH vuông góc với SC=> SC vuông góc với (BHK)+) SC vuông góc với BKSA vuông góc với BH=> (SAC) vuông góc với (BHK)
|
|
|
|
giải đáp
|
hình hoc không gian
|
|
|
|
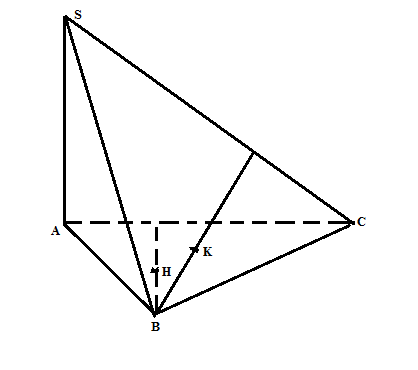 a/ +)K là trực tâm $\Delta$ SBC => SC vuông góc với BK H là trực tâm $\Delta$ ABC=> BH vuông góc với SC => SC vuông góc với (BHK) +) SC vuông góc với BK SA vuông góc với BH => (SAC) vuông góc với (BHK) |
|
|
|
bình luận
|
hình hoc không gian
Mình nghĩ là H và K lần lượt là trực tâm của các tam giác trên, là trọng tâm thì vô lý!
|
|
|
|
|
|
|
|
giải đáp
|
1 bài hình học không gian
|
|
|
|
b/ $\Delta$ SB'A đồng dạng với $\Delta$SAB (g-g)
=> $\frac{SB'}{SA}$=$\frac{SA}{SB}$ => SB'. SB= $SA^{2}$
$\Delta$ SC'A đồng dạng với $\Delta$SAC (g-g)
=> $\frac{SC'}{SA}$=$\frac{SA}{SC}$ => SC'. SC= $SA^{2}$
$\Delta$ SD'A đồng dạng với $\Delta$SAD (g-g)
=> $\frac{SD'}{SA}$=$\frac{SA}{SD}$ => SD'. SD= $SA^{2}$
=> đpcm
|
|