|
|
được thưởng
|
Đăng nhập hàng ngày 01/12/2015
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 29/11/2015
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 28/11/2015
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 24/11/2015
|
|
|
|
|
|
|
|
được thưởng
|
Đăng nhập hàng ngày 22/11/2015
|
|
|
|
|
|
|
|
giải đáp
|
help me!!!!!!!!!!
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
tim m de phuong trinh
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Rút gọn giúp em với
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
Bất phương trình
|
|
|
|
Bổ đề: x,y,z>0 cmr x+y+z≥3xyz−−−√3 (1)
Cm: Đặt x=a3,y=b3,z=c3⇒(1)⇔a3+b3+c3−3abc≥0
⇔(a+b+c).12[(a−b)2+(b−c)2+(c−a)2]≥0
Hiển nhiên do x,y,z>0⇒a,b,c>0 và 12[(a−b)2+(b−c)2+(c−a)2]≥0 dấu = khi a=b=c⇒x=y=z
Áp dụng BDT xy+yz+zx≤x2+y2+z2 và x+y+z≥3xyz−−−√3
Do đó A≥3xyz−−−√3+4xyz1+4(x2+y2+z2) (2)
Mặt khác x2+y2+z2=1−16xyz4
Thay vào (2) suy ra A≥3xyz−−−√3+4xyz1+4(x2+y2+z2)=3xyz−−−√3+4xyz1+4(1−16xyz4)=3xyz−−−√3+4xyz2(1−8xyz)
Đặt xyz−−−√3=k
Suy ra A≥3k+4k32(1−8k3)
Mặt khác nhận thấy từ điều kiện x2+y2+z2=1−16xyz4⇒4(x2+y2+z2)+16xyz=1
1=4(x2+y2+z2)+16xyz≥12x2y2z2−−−−−−√3+16xyz (áp dụng bổ đề)
↔12x2y2z2−−−−−−√3+16xyz−1≤0⇒12k2+16k3−1≤0⇒(k−14).(k+12)2≤0
Do đó k−14≤0 (do (k+12)2≥0)
Như vậy k≤14 mà x,y,z>0⇒0<k<14
Mặt khác A≥3k+4k32(1−8k3) với mọi 0<k≤14
Suy ra A≥max(3k+4k32(1−8k3)) với 0<k≤14 (ta làm được điều này do 0<k≤14 là tập xác định)
Ta sẽ chứng minh max(3k+4k32(1−8k3))=1328
⇔28(3k+4k3)≤26(1−8k3)
⇔320k3+84k−26≤0
⇔2(4k−1)(40k2+10k+13)≤0
⇔(4k−1)≤0 (do 40k2+10k+13=40(k2+14k+1340)=40((k+18)2+99320)>0)
⇔k≤14 đúng do ta đã cm trên
Suy ra max(3k+4k32(1−8k3))=1328⇒A≥1328
Dấu = khi x=y=z và k=xyz−−−√3=14⇒x=y=z=14
|
|
|
|
giải đáp
|
Toán 10 Vector
|
|
|
|
theo bài ra ta suy ra P,Q,R thuộc 3 cạnh $\Delta $ABC $\rightarrow $ bạn sd định lí Meneelauyts là ra k=$\frac{9}{8}$ Nộ dung định lý:Cho tam giác ABC. D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó định lý phát biểu rằng D, E, F thẳng hàng khi và chỉ khi 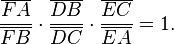
|
|
|
|
giải đáp
|
Tìm m
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
sửa đổi
|
RÚT GỌN CĂN BẬC HAI THEO HẰNG ĐẲNG THỨC SỐ 1 VÀ 2
|
|
|
|
a// D=$\frac{2}{\sqrt{32}+\sqrt{6+2\sqrt{5}}}$=$\frac{2}{\sqrt{32}+\sqrt{5}+1}$b// B=($\sqrt{a}$+$\sqrt{b}$)-$\frac{1}{\sqrt[3]{a^{2}+....}}$ (sd HĐT số7)=.........
a// D=$\frac{2}{\sqrt{32}+\sqrt{6+2\sqrt{5}}}$=$\frac{2}{\sqrt{32}+\sqrt{5}+1}$b// B=($\sqrt{a}$+$\sqrt{b}$)-$\frac{1}{\sqrt[3]{a^{2}}+...}$ (sd HĐT số7)=.........
|
|
|
|
|
|
giải đáp
|
ai giup tui zoi
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|