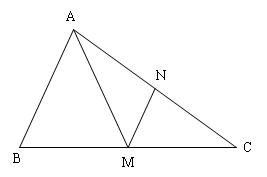
Đỉnh $A$ là giao điểm của hai cạnh $AB; AC$ nên tọa độ $A$ là nghiệm của hệ
$\begin{cases}x-2y-2=0 \\2x+5y+3=0 \end{cases} \Leftrightarrow \begin{cases}x=\frac{4}{9} \\ y=-\frac{7}{9} \end{cases} \Rightarrow A(\frac{4}{9};-\frac{7}{9} )$
Đường thẳng $d$ đi qua $M$ và song song với $AB$ có phương trình là :
$1.(x+2)-2(y-2)=0\Leftrightarrow x-2y+6=0$
Đường thẳng $d$ cắt $AC$ tại $N$.Tọa độ của $N$ là nghiệm của hệ :
$\begin{cases}x-2y+6=0 \\ 2x+5y+3=0 \end{cases} \Leftrightarrow \begin{cases}x=-4 \\ y=1 \end{cases} \Rightarrow N(-4;1)$
Do $N(-4;1)$ là trung điểm của cạnh $AC$ nên :
$x_N=\frac{x_A+x_C}{2} $ và $y_N=\frac{y_A+y_C}{2} $
Suy ra : $x_C=2x_N-x_A=2(-4)-\frac{4}{9} =-\frac{76}{9} $
$y_C=2y_N-y_A=2.1-(-\frac{7}{9} )=\frac{25}{9} \Rightarrow C(-\frac{76}{9};\frac{25}{9})$
$M(-2;2)$ là trung điểm của $BC$ nên : $x_M=\frac{x_B+x_C}{2} $ và $y_M=\frac{y_B+y_C}{2} $
$\Rightarrow \begin{cases}x_B=2x_M-x_C=2(-2)-(-\frac{76}{9} )=\frac{40}{9} \\ y_B=2y_M-y_C=2.2-\frac{25}{9}=\frac{11}{9} \end{cases} $
Vậy tọa độ các đỉnh của tam giác $ABC $ là :
$A(\frac{4}{9};-\frac{7}{9} ); B(\frac{40}{9};\frac{11}{9} );C(-\frac{76}{9};\frac{25}{9} )$