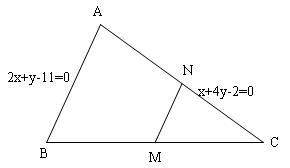
$a.$ $A$ là giao điểm của cạnh $AB$ và $AC$ nên tọa độ của $A$ là nghiệm của hệ phương trình :$\begin{cases}2x+y-11=0 \\ x+4y-2=0 \end{cases} \Leftrightarrow \begin{cases}x_A=6 \\ y_A=-1 \end{cases} \Rightarrow A(6;-1)$
$b.$ $MN//AB$ nên phương trình đường thẳng $MN$ có dạng : $2x+y+C=0$
Đường thẳng $MN$ qua $M(0;4)$ nên $2.0+4+C=0\Rightarrow C=-4$
Phương trình đường thẳng $MN$ là $2x+y-4=0$
Tọa độ $N$ là nghiệm của hệ phương trình :
$\begin{cases}x+4y-2=0 \\ 2x+y-4=0 \end{cases} \Leftrightarrow \begin{cases}x_N=2 \\ y_N=0 \end{cases} \Rightarrow N(2,0)$
$N$ là trung điểm của $AC$ nên :
$x_N=\frac{x_A+x_C}{2}\Rightarrow x_C=2x_N-x_A=4-6=-2 $
$y_N=\frac{y_A+y_C}{2} \Rightarrow y_C=2y_N-y_A=0-(-1)=1$
Tọa độ của đỉnh $C$ là $C(-2,1)$
Tương tự $M$ là trung điểm của $BC$ nên :
$x_M=\frac{x_B+x_C}{2}\Rightarrow x_B=2x_M-x_C=0-(-2)=2 $
$y_M=\frac{y_B+y_C}{2}\Rightarrow y_B=2y_M-y_C=8-1=7 $
Tọa độ của đỉnh $B$ là $B(2,7)$
Vậy tọa độ các đỉnh của tam giác $ABC$ là $A(6;-1),B(2;7),C(-2;-1)$