|
|
1 . Các bước khảo sát sự biến thiên và vẽ đồ thi của hàm số
1) Tìm tập xác định của hàm số
2) Xét sự biến thiên của hàm số
a) Tìm giới hạn tại vô cực và giới hạn vô cực (nếu có) của hàm số ,tìm đường tiệm cận của đồ thị nếu có
b) Lập bảng biên thiên của hàm số bao gồm
Tìm đạo hàm của hàm số, xết dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số ( nếu có), điền các kết quả vào bảng
3) Vẽ đồ thị của hàm số
- Vẽ các đường tiệm cận của đồ thị ( nếu có )
- Xác định 1 số điểm đặc biệt của đồ thị, chẳng hạn giao điểm của đồ thị với các trục tọa độ
- Nhận xét về đồ thị: chỉ ra trục và tâm đối xứng của đồ thị ( nếu có )
2 . Hàm số $y = {\text{a}}{{\text{x}}^3} + b{x^2} + cx + d\,\,\,\,\,\,\,\,(a \ne 0)$
VÍ DỤ
Khảo sát sự biên thiên và vẽ đồ thị (C) của hàm số
$y = \frac{1}{8}(x^3-3x^2-9x-5) $
Giải
1) Hàm số có tập hợp xác định là $R$
2) Sự biến thiên của hàm số
a) Giới hạn của hàm số tại vô cực
$\mathop {\lim y = - \infty}\limits_{x \to - \infty } $ và $\mathop {\lim y = + \infty }\limits_{x \to + \infty } $
b) Bảng biến thiên
ta có
$\begin{gathered}
y' = \frac{1}{8}{\text{(}}3{x^2} - 6x - 9); \\
y' = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow x = - 1\,;\,\,x = 3 \\
\end{gathered} $
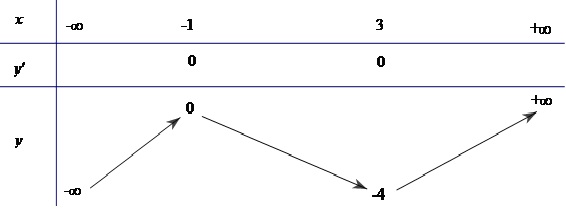
Hàm số đồng biến trên khoảng $( -8 ; 1)$ và $( 3 ;+8)$ nghịch biến trên khoảng $(-1 3)$ Hàm số đạt cực đại tại điểm $x = 1$ ; giá trị cực đại của hàm số là $y (-1) = 0$ ,
Hàm số đạt cực tiểu tại điểm $x = 3$ ; giá trị cực tiểu của hàm số là $y(3) = -4$
3) Đồ thị :
Giao điểm của đồ thị với trục tung là điểm $\left( {0;\frac{5}{8}} \right)$ .Ta có
$y = 0$ $ \Leftrightarrow {(x + 1)^2}(x - 5) = 0$
$ \Leftrightarrow x = - 1;x = 5$
Vậy đồ thị và trục hoành có hai điểm chung $(-1 ;0)$ và $(5 ;0)$
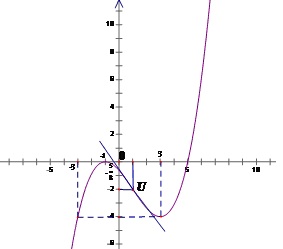
Ngoài ra, ta có khái niệm điểm uốn như sau:
Điểm $U({x_0};{y_0})$ được gọi là điểm uốn của đồ thị hàm số $y = f(x)$ nếu tồn tại 1 khoảng (a;b) chứa điểm ${x_0}$ sao cho trên 1 trong 2 khoảng $(a;{x_0})\& ({x_0};b)$ tiếp tuyến của đồ thị hàm số tại U nằm phía trên đồ thị còn trên khoảng kia tiếp tuyến nằm phía dưới đồ thị
Để tìm điểm uốn, ta sử dụng khẳng định sau:
- Nếu hàm số $y = f(x)$ có đạo hàm cấp 2 trên 1 khoảng chứa điểm ${x_0}$; $f''({x_0}) = 0$ và $f'(x)$ đổi dấu khi đi qua điểm ${x_0}$ thì $U({x_0};f({x_0}))$ là 1 điểm uốn của đồ thị $y = f(x)$
- Đồ thị hàm số bậc ba $ f(x) = ax^3+ b{x^2} + cx + d\,\,\,\,(a \ne 0)$ luôn có 1 điểm uốn và điểm đó là tâm đối xứng của đồ thị
3. Hàm số trùng phương $y = a{x^4} + b{x^2} + c\,\,\,(a \ne 0)$
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = {x^4} - 2{x^2} - 3$
Giải:
1. Hàm số có tập xác định là $R$
2. Sự biến thiên của hàm số
a) Giới hạn của hàm số tại vô cực:
$\mathop {\lim y = + \infty}\limits_{x \to - \infty } \& \mathop {\lim y = + \infty}\limits_{x \to + \infty } $
b) Bảng biến thiên:
Ta có:
$\begin{gathered}
y' = 4x({x^2} - 1) \\
y' = 0 \Leftrightarrow x = 0;x = 1;x = - 1 \\
\end{gathered} $
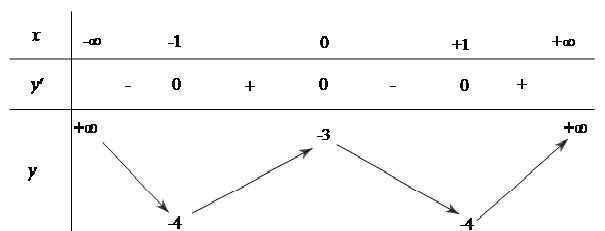
Hàm số nghịch biến trên mỗi khoảng $( - \infty ; - 1)\& (0;1)$ và đồng biến trên mỗi khoảng $( - 1;0)\& (1; + \infty )$
Hàm số đạt cực đại tại x=0, giá trị cực đại là $y(0) = - 3$
Hàm số đạt cực tiểu tại các điểm $x = \pm 1$, giá trị cực tiểu là $y( \pm 1) = - 4$
3. Đồ thị:
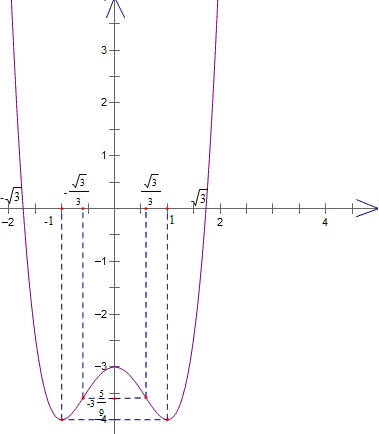
- Điểm uốn:
Ta có: $y'' = 12{x^2} - 4$
$y'' = 0$ tại các điểm ${x_1} = \frac{{\sqrt 3 }}{3};{x_2} = - \frac{{\sqrt 3 }}{3}$ và đổi dấu khi x đi qua mỗi điểm đó
Do vậy ${U_1}\left( { - \frac{{\sqrt 3 }}{3}; - 3\frac{5}{9}} \right)$ và ${U_2}\left( {\frac{{\sqrt 3 }}{3}; - 3\frac{5}{9}} \right)$ là 2 điểm uốn của đồ thị
- Giao điểm của đồ thị với trục tung là điểm (0;-3)
Ta có: $y = 0 \Leftrightarrow x = \pm \sqrt 3 $
Vậy đồ thị cắt trục hoành tại 2 điểm $( - \sqrt 3 ;0)\& (\sqrt 3 ;0)$
CHÚ Ý
Gọi $(C)$ là đồ thị của hàm số $y = ax^4+bx^2+c (a \neq 0)$
Người ta chứng minh được rằng
1) Nếu phương trình $f''(x) = 0$ có hai nghiệm phân biệt $x = \pm {x_0}({x_0} > 0)$thì đồ thị $(C)$ có hai điểm uốn ${U_1}({x_0};f({x_0}))$ và ${U_2}( - {x_0};f( - {x_0}))$${x_0}$ đối xứng với nhau qua hai trục tung.
2) Nếu phương trình $(1)$ có một nghiệm kép hoặc vô nghiệm thì đồ thị $(C)$ không có điểm uốn.
|