|
|
1.ĐỊNH NGHĨA
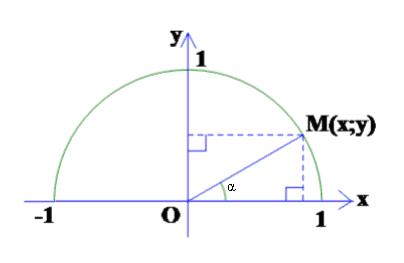
Với mỗi góc $\alpha \,\,\left( {{0^0} \leqslant \alpha \leqslant {{180}^0}} \right)$, ta xác định điểm M trên nửa đường tròn đơn vị sao cho $\angle MOx = \alpha $. Giả sử điểm M có tọa độ $(x; y)$. Khi đó
Tung độ y của điểm M gọi là sin của góc $\alpha $, kí hiệu là $\sin \alpha$. Hoành độ $x$ của điểm $M$ gọi là côsin của góc $\alpha $, kí hiệu là cos$\alpha $;
Tỉ số $\frac{y}{x}$ ( với$x \ne 0$) gọi là tang của góc $\alpha $, kí hiệu là tan$\alpha $
Tỉ số $\frac{x}{y}$ ( với $y \ne 0$) gọi là côtang của góc$\alpha $, kí hiệu là cot$\alpha $
Ví dụ: Tìm các giá trị lượng giác của góc ${135^0}$
Giải:
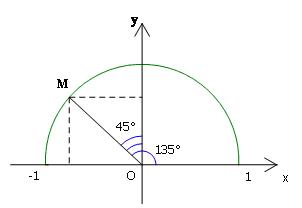
Ta lấy điểm M trên đường tròn đơn vị sao cho $\angle MOx = {135^0}$. Khi đó hiển nhiên $\angle Moy = {45^0}$. Từ đó suy ra tọa độ của điểm M là
$M\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)$
Vậy $\sin {135^0} = \frac{{\sqrt 2 }}{2};\,\cos {135^0} = - \frac{{\sqrt 2 }}{2}\,;\tan {135^0} = - 1;\cot {135^0} = - 1$.
Từ đó suy ra :
Nếu hai góc bù nhau thì sin của chúng bằng nhau ,còn côsin ,tang và côtang của chúng đối nhau, nghĩa là:
$sin(180^0-\alpha)=sin \alpha;$
$cos(180^0-\alpha)=-cos \alpha;$
$tan(180^0-\alpha)=-tan \alpha (\alpha \neq 90^0);$
$tan(180^0-\alpha)=-cot \alpha (0^0<\alpha<180^0)$;
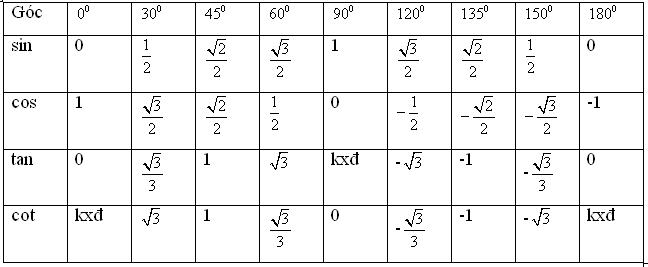
2. Giá trị lượng giác của một số góc đặc biệt
|