|
|
1.Góc giữa hai vectơ
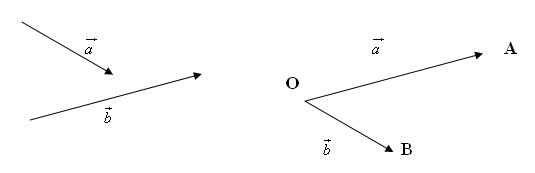
Cho 2 vecto $\overrightarrow {a\,} \& \overrightarrow b $ đều khác 0. Từ 1 điểm O nào đó vẽ $\overrightarrow {OA} = \overrightarrow {a\,} \& \overrightarrow {OB} = \overrightarrow b $
- Số đo của góc AOB được gọi là số đo của góc giữa $\overrightarrow a $ và $\overrightarrow b $, hoặc đơn giản là góc giữa hai vectơ$\overrightarrow a $ và $\overrightarrow b $
- Nếu $\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^ \circ }$ thì ta nói rằng hai vectơ $\overrightarrow a $ và $\overrightarrow b $ vuông góc với nhau, kí hiệu là $\overrightarrow a \bot \overrightarrow b $.
2. Định nghĩa tích vô hướng cả hai vectơ
Tích vô hướng của hai vectơ $\overrightarrow a $ và $\overrightarrow b $ là một số, kí hiệu $\overrightarrow a .\overrightarrow b $, được xác định bởi
$\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|c{\text{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)$
Ví dụ:
Cho tam giác đều ABC có cạnh a và trọng tâm G .Tính các tích vô hướng sau
$\begin{gathered}
\overrightarrow {AB} .\overrightarrow {AC} ;\,\,\overrightarrow {AC} .\overrightarrow {CB} \,\,;\,\,\,\overrightarrow {AG} .\overrightarrow {AB} \\
\overrightarrow {GB} .\overrightarrow {GC} ;\,\,\,\overrightarrow {BG} .\overrightarrow {GA} \,;\,\,\,\,\overrightarrow {GA} .\overrightarrow {BC} \\
\end{gathered} $
Giải.
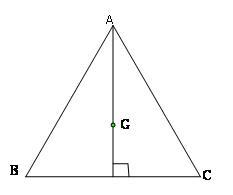
Theo định nghĩa ta có
$\begin{gathered}
\overrightarrow {AB} .\overrightarrow {AC} \, = \,a.a.c{\text{os}}{60^0} = \frac{1}{2}{a^2} \\
\overrightarrow {AC} .\overrightarrow {CB} \, = \,a.a.c{\text{os12}}{{\text{0}}^0} = - \frac{1}{2}{a^2} \\
\overrightarrow {AG} .\overrightarrow {AB} = \,a\frac{{\sqrt 3 }}{3}.a.c{\text{os3}}{0^0} = {a^2}\frac{{\sqrt 3 }}{3}.\frac{{\sqrt 3 }}{3} = \frac{1}{2}{a^2}; \\
\overrightarrow {GB} .\overrightarrow {GC} = a\frac{{\sqrt 3 }}{3}.a\frac{{\sqrt 3 }}{3}.c{\text{os12}}{{\text{0}}^0} = \frac{{{a^2}}}{6};\,\,\, \\
\overrightarrow {BG} .\overrightarrow {GA} \, = a\frac{{\sqrt 3 }}{3}.a\frac{{\sqrt 3 }}{3}.c{\text{os6}}{{\text{0}}^0} = \frac{{{a^2}}}{6};\, \\
\overrightarrow {GA} .\overrightarrow {BC} = a\frac{{\sqrt 3 }}{3}.a.c{\text{os9}}{{\text{0}}^0} = 0;\, \\
\end{gathered} $
Bình phương vô hướng
Bình phương vô hương của một vectơ bằng bình phương độ dài của vectơ đó
3. Tính chất của tính vô hướng
Định lí
Với ba vectơ$\overrightarrow a $,$\overrightarrow b $, $\overrightarrow c $tuỳ ý và mọi số thưc k ,ta có
1)$\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a $ (tính chất giao hoán);
2)$\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \overrightarrow a \bot \overrightarrow b $
3)$(k\overrightarrow a ).\overrightarrow b = \overrightarrow a .(k\overrightarrow b ) = k(\overrightarrow a .\overrightarrow b );$
4) $\overrightarrow a .(\overrightarrow b + \overrightarrow c ) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c $ (tính chất phân phối đối với phép cộng);
$\overrightarrow a .(\overrightarrow b - \overrightarrow c ) = \overrightarrow a .\overrightarrow b - \overrightarrow a .\overrightarrow c $ (tính chất phân phối đối với phép trừ);
Bài toán 1: Cho tứ giác ABCD
a, Chứng minh rằng
$A{B^2} + C{D^2} = B{C^2} + A{D^2} + 2\overrightarrow {CA} .\overrightarrow {BD} $
b, Từ câu a), hãy chứng minh rằng: Điều kiện cần và đủ để tứ giác có hai đường thẳng chéo vuông góc là tổng bình phương các cặp cạnh đối diện bằng nhau.
Giải

a, Ta có
$\begin{gathered}
A{B^2} + C{D^2} - B{C^2} - A{D^2} \\
= {(\overrightarrow {CB} - \overrightarrow {CA} )^2} + C{D^2} - C{B^2} - {(\overrightarrow {CD} - \overrightarrow {CA} )^2} \\
= \,\, - 2\overrightarrow {CB} .\overrightarrow {CA} \,\, + 2\overrightarrow {CD} .\overrightarrow {CA} \\
= 2\overrightarrow {CA} .(\overrightarrow {CD} - \overrightarrow {CB} ) = 2\overrightarrow {CA} .\overrightarrow {BD} \\
\end{gathered} $
Từ đó suy ra điều phải chứng minh
b, Từ a ta có ngay
$CA \bot BD \Leftrightarrow \overrightarrow {CA} .\overrightarrow {BD} \Leftrightarrow A{B^2} + C{D^2} = B{C^2} + A{D^2}$
CHÚ Ý
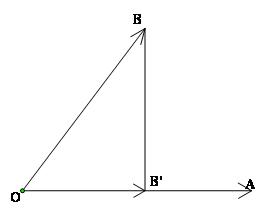
1)Cho 2 vecto $\overrightarrow {OA} ,\overrightarrow {OB} $. Gọi B’ là hình chiếu của B trên đường thằng OA. Khi đó:
- Vecto $\overrightarrow {OB'} $gọi là hình chiếu của vecto $\overrightarrow {OB} $ trên đường thằng OA
- Công thức $\overrightarrow {OA} .\overrightarrow {OB} = \overrightarrow {OA} .\overrightarrow {OB'} $ gọi là công thức hình chiếu
2) Cho đường tròn (O;R) và điểm M cố định. Một đường thẳng thay đổi đi qua M, cắt đường tròn đó tại 2 điểm A và B.

Khi đó, giá trị không đổi $\overrightarrow {MA} .\overrightarrow {MB} = {d^2} - {R^2}\,\,\,\,(d = MO)$ gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là ${(P)_{M/(O)}}$
${(P)_{M/(O)}} = \overrightarrow {MA} .\overrightarrow {MB} = {d^2} - {R^2}(d = MO)$
3) Khi điểm M nằm ngoài đường tròn (O), MT là tiếp tuyến của đường tròn đó ( T là tiếp điểm) thì
${(P)_{M/(O)}} = {\overrightarrow {MT} ^2} = M{T^2}$
4. Biểu thức tọa độ của tích vô hướng
Các hệ thức quan trọng
Cho hai vectơ $\overrightarrow b = \left( {x';y'} \right)$và $\overrightarrow b = \left( {x';y'} \right)$
1)$\overrightarrow a .\overrightarrow b = xx' + yy'$
2) $\left| {\overrightarrow a } \right| = \sqrt {{x^2} + {y^2}} $
3) $c{\text{os}}(\overrightarrow a ,\overrightarrow b ) = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} \sqrt {{x^{'2}} + y{'^2}} }}\,\,\,\,\,(\overrightarrow a \ne 0,\overrightarrow b \ne 0)$
Đặc biệt: $\overrightarrow a \bot \overrightarrow b \Leftrightarrow xx' + yy' = 0$
HỆ QUẢ
Trong mặt phẳng toạ độ, khoảng cách giữa hai điểm $M({x_M};{y_M})$ và $N({x_N};{y_N})$ là
$MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{({x_N} - {x_M})}^2} + {{({y_N} - {y_M})}^2}} $
|