|
|
1. Phương trình đường tròn
Trên mặt phẳng tọa độ, cho đường tròn (C ) có tâm $I({x_0};{y_0})$ và bán kính R
Ta có : 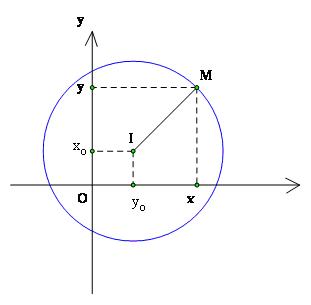
Điểm $M(x;y)$thuộc đường tròn (C ) khi và chỉ khi IM = R, hay là
${(x - {x_0})^2} + {(y - {y_0})^2} = {R^2}$ (1)
Ta gọi phương trình (1) là phương trình của đường tròn (C )
2. Nhận dạng phương trình đường tròn
Phương trình ${x^2} + {y^2} + 2{\text{ax}} + 2by + c = 0$với điều kiện ${a^2} + {b^2} > c$ à phương trình của đường tròn tâm $I( - a; - b)$bán kính ${R^2} = \sqrt {{a^2} + {b^2} - c} $
VÍ DỤ
Viết phương trình đường tròn đi qua điểm $M (1;2 ) , N(5: 5 )$ và $P ( 1 ;-3)$
Giải
Gọi $I (x,y )$ và $R$ là tâm và bán kính của đường tròn đi qua ba điểm $M,N,P$
từ điều kiện IM = IN = IP ta có hệ phương trình.
$\begin{cases}(x-1)^{2}+(y-2)^{2}=(x-5)^{2}+(y-2)^{2} \\ (x-1)^{2}+(y-2)^{2}=(x-1)^{2}+(y+3)^{2} \end{cases} $
Dễ dàng tìm được nghiệm hệ là x = 3 ,y = - 0,5. vậy I = (3;- 0,5) khi đó ${R^2} = I{M^2} = 10,25$. Phương trình đường tròn cần tìm là
${(x - 3)^2} + {(y + 0,5)^2} = 10,25$
3. Phương trình tiếp tuyến của đường tròn
Để viết phương trình tiếp tuyến của đường tròn, ta thường dùng điều kiện như sau ; Đường thẳng tiếp xúc với đường tròn khi và chỉ khi khoảng cách từ tâm đường tròn đến đường thẳng bán kính của đường tròn
Tuy nhiên, để viết phương trình tiếp tuyến của đường tròn tại điểm M cho trước thuộc đường tròn, ta có cách giải đơn giản hơn.
Bài toán: Cho đường tròn ${x^2} + {y^2} - 2x + 4y - 20 = 0$ và điểm $M(4;2)$
a) Chứng tỏ rằng điểm M nằm trên đường tròn đã cho
b) Viết phương trình tiếp tuyến của đường tròn tại điểm M
Giải:
a) Thay tọa độ điểm M vào vế trái của phương trình đường tròn ta được:
${4^2} + {2^2} - 2.4 + 4.2 - 20 = 0$
Vậy M nằm trên đường tròn
b) Đường tròn có tâm $I(1; - 2)$. Tiếp tuyến của đường tròn tại M là đường thẳng đi qua M và nhận $\overrightarrow {MI} $ làm vecto pháp tuyến
Vì $\overrightarrow {MI} = ( - 3; - 4)$nên phương trình tiếp tuyến là:
$ - 3(x - 4) - 4(y - 2) = 0 \Leftrightarrow 3x + 4y - 20 = 0$
|