|
|
1. Phép vị tự trong không gian
- Định nghĩa 1: Cho số k khác 0 và 1 điểm O cố định. Phép biến hình trong không gian biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow {OM} = k\overrightarrow {OM'} $ gọi là phép vị tự. Điểm O gọi là tâm vị tự, k gọi là tỉ số vị tự
Các tính chất cơ bản của phép vị tự
- Nếu phép vị tự tỉ số k biến 2 điểm M, N thành 2 điểm M’, N’ thì $\overrightarrow {M'N'} = k\overrightarrow {MN} $ và do đó $M'N' = \left| k \right|MN $
- Phép vị tự biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng, 4 điểm đồng phẳng thành 4 điểm đồng phẳng
Từ đó suy ra phép vị tự biến đường thẳng thành đường thẳng, mặt phẳng thành mặt phẳng…
Ví dụ:
Cho tứ diện ABCD. Gọi A’, B’, C’, D’ lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng có phép vị tự biến tứ diện ABCD thành tứ diện A’B’C’D’
Giải:
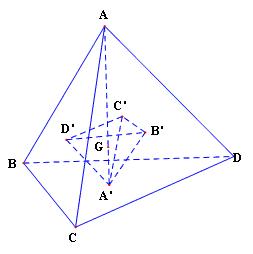
Gọi G là trọng tâm tứ diện ABCD. Ta có
$\begin{gathered}
\overrightarrow {GA'} = - \frac{1}{3}\overrightarrow {GA} ,\,\overrightarrow {GB'} = - \frac{1}{3}\overrightarrow {GB} \\
\overrightarrow {GC'} = - \frac{1}{3}\overrightarrow {GC} ,\,\overrightarrow {GD'} = - \frac{1}{3}\overrightarrow {GD} \\
\end{gathered} $
Suy ra phép vị tự V tâm G, tỉ số $k = - \frac{1}{3} $ biến các điểm A,B,C,D lần lượt thành các điểm A’,B’,C’,D’. Vậy V biến tứ diện ABCD thành tứ diện A’B’C’D’
2. Hai hình đồng dạng
• Định nghĩa 2: Hình (H) được gọi là đồng dạng với hình (H’) nếu có 1 phép vị tự biến hình (H) thành hình ( ${H_1} $) mà hình ( ${H_1} $) bằng hình (H’)
Như vậy ta có thể thấy:
- Hai hình tứ diện đều bất kỳ luôn đồng dạng với nhau
- Hai hình lập phương bất kỳ đều đồng dạng với nhau
3. Khối đa diện đều và sự đồng dạng của các khối đa diện đều
- Một khối đa diện được gọi là khối đa diện lồi nếu với bất kỳ 2 điểm A và B nào của nó thì mọi điểm của đoạn thẳng AB cũng thuộc khối đó
- Định nghĩa khối đa diện đều: Khối đa diện đều là 1 khối đa diện lồi có 2 tính chất sau đây:
a) Các mặt là những đa giác đều có cùng số cạnh
b) Mỗi đỉnh là đỉnh chung của cùng 1 số cạnh
- Khối đa diện đều mà mỗi mặt là đa giác đều n cạnh và mỗi đỉnh là đỉnh chung của p cạnh được gọi là khối đa diện đều loại {n,p}
|