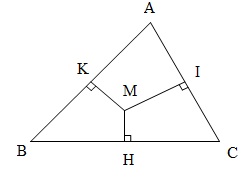
Với mọi tam giác $ABC$ và điểm $M$ trong tam giác ta có
$\left\{ \begin{array}{l}
{S_a}\overrightarrow {MA}  + {S_b}\overrightarrow {Mb}  + {S_c}\overrightarrow {MC}  = \overrightarrow 0 \,\,\,\,\,\,\,\,\,\, &  &  & (1)\\
\frac{a}{{MH}}\overrightarrow {MH}  + \frac{b}{{MI}}\overrightarrow {MI}  + \frac{c}{{MK}}\overrightarrow {MK}  = \overrightarrow 0  &  &  & (2)
\end{array} \right.$

Biến đổi tương đương:
$M$ là trọng tâm $\Delta ABC$
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \\
 \Leftrightarrow {S_a} = {S_b} = {S_c}\\
 \Leftrightarrow a.MH = b.MI = c.MK\\
 \Leftrightarrow \frac{{{a^2}}}{({\frac{a}{{MH}}})} = \frac{{{b^2}}}{({\frac{b}{{MI}}})} = \frac{{{c^2}}}{({\frac{c}{{MK}}})}
\end{array}\)
   \( \Leftrightarrow {a^2}\overrightarrow {MH}  + {b^2}\overrightarrow {MI}  + {c^2}\overrightarrow {MK}  = \overrightarrow 0 \)( theo $(2)$).

Giải phương trình
$11\cos^{2008}x+2012\sin^{2010}x=2012$

Cho hàm số : $y=x^4-2(m-2)x^2+2m+3$. Tìm $m$ để đồ thị hàm số cắt $Ox$ tại  $4$ điển phân biệt có hoành độ theo thứ tự lập thành cấp số cộng

Tìm Max- Min : $y=\frac{\sqrt{\cos(x-\frac{\pi}{7} )} }{\sin x+\sqrt{3-2\sin^2x} } $ với $x\in [\frac{\pi}{2} ;\pi]$

Tìm $m$ để đồ thị hàm số $y=x^3+2x^2+mx$ có điểm $CT,CĐ$ đối xứng qua đường thẳng $x+2y=0$

Cho $y=\frac{x-m}{x-2} $ cho $2$ điểm $A, B$ thuộc đồ thị sao cho $2$ tiếp tuyến tại $A, B$ song song nhau. Tìm trung điểm $AB?$

Cho hàm số $y=x^3-3(m+1)x^2+2(m^2+7m+2)x-2m(m+2)$. Tìm m để $y=0$ có nghiệm phân biệt $\geq  1$

Giải hệ phương trình : $\begin{cases}x^3y-y^4=28\\x^2y+2xy^2+y^3=18\sqrt{2} \end{cases} $

Giải phương trình : $2(\cot 2x-\cot 3x)=\tan 2x+\cot 3x$

Giải phương trình :  $\cot x+\sqrt{2\cot2x+\tan x+3}=3 $