Lời giải của m khá dài và chủ yếu là m khá lười :) m nêu vắn tắt cách làm bạn tham khảo nhé (cách này khá trâu bò)
a, Nhân cả tử và mẫu với sinx rồi chia cho $cosx^{4}$
ta có $I=\int\limits_{0}^{\pi/4}\frac{tanx+5-5}{tanx^{2}+5tanx+1}dtanx$
sau đó bạn tách làm hai tích phân cái đầu hàm hợi cái sau lượng giác hoá
b,Đua về  cos2x  $I=-1/4\int\limits_{0}^{\pi/2}\frac{1-cos2x}{1+cos2x^{2}}dcos2x$
tách ra 2 tích phân xét $I_1=\int\limits_{0}^{\pi/2}\frac{cos2x}{1+cos2x^{2}}dcos2x$
$I_2=\frac{1}{1+cos2x^{2}}$
cái đầu hàm hợp cái hai lượng giác hoá đặt $cos2x=tan\alpha$

$f'(x)=6x^{2}+8x$
tiếp tuyến song song với $d$ toạ độ tiếp diểm là nghiệm $f'(x)=k=-2$
$\Rightarrow x=-1 f(-1)=5$
$ x=-1/3  f(-1/3)=91/27$
tt có dạng 
 $y=-2.(x-x_0)+y_0$

Gọi $N$ là trung điểm của $AC$
$MN$ qua $M(1/2;4)$  vuông góc với $h_A=> MN:  x+3y-25/2=0$
Gọi $N(25/2-3a;a) \in MN  $ có ĐK $a>\tfrac{17}{4} (M,N  $  nằm khác phía so với $h_A)$
$MN=\tfrac{\sqrt{10}}{2}\Rightarrow N(-1;\tfrac{9}{2})$
Gọi $A(b;3b+5)\rightarrow B(1-b;3-3b)\Rightarrow $vecto $AN$.vecto$BH=0=>b$

$I=\int\limits_{0}^{\pi/2}\sqrt{3cosx^{2}-2.\sqrt{3}.cosx.sinx+sinx^{2}}=\int\limits_{0}^{\pi/2}|sin(x-\pi/3)|dx$
$I=-\int\limits_{0}^{\pi/3}sin(x-\pi/3)d(x-\pi/3)+\int\limits_{\pi/3}^{\pi/2}sin(x-\pi/3)d(x-\pi/3)$
Đến đây b có thể tự làm nốt nhé:)

M không nhớ số liệu nên cho bài toán dưới dạng tổng quá nhé !!!
Tam giác $ABC$ cho toạ độ tâm đường tròn nội tiếp và ngoại tiếp lần lượt là $I,J$
và cho toạ độ đỉnh $A$ tìm toạ độ $B,C$

$4sin2x^{2}+sin6x^{2}-4sin2x.sin6x^{2}=0$

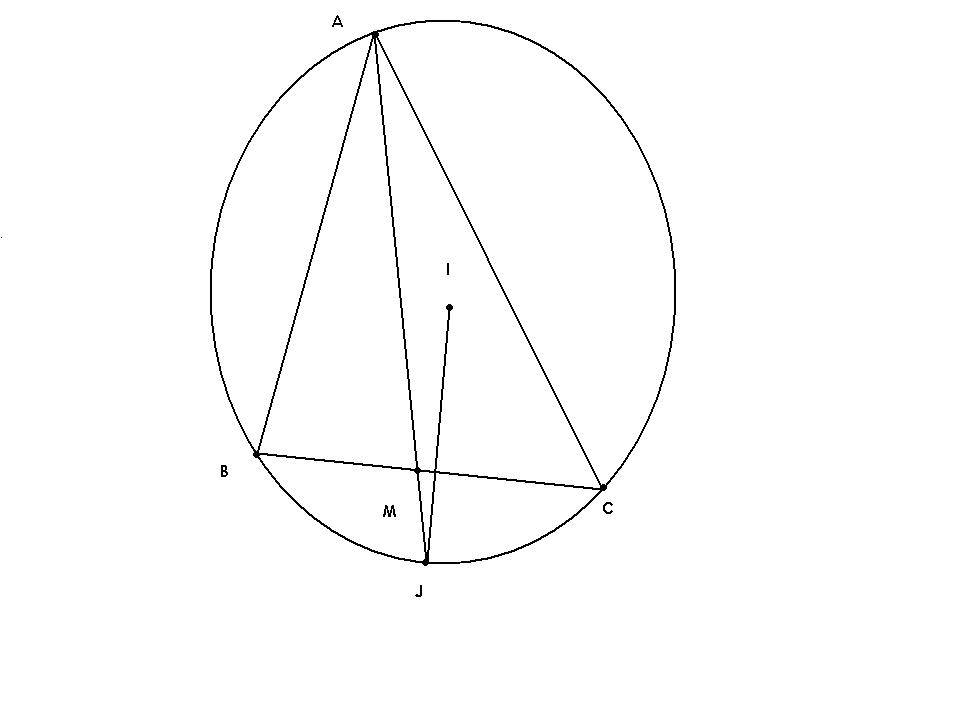Tóm tắt cách giải
lập pt $(C)$ có tâm $I$ và $R=IA$
lập phương trình $AM$
Gọi $J=AM\cap (C)$
$BC$ qua $M$ và vuông góc với $IJ$

ta có $A(0;-4;-1)$ nằm ở hai mặt phẳng $(P) (Q)$
$(P)$ có VTPT $n_1(1;-1;-1)$
$(Q)$ có VTPT $n_2(2;1;3)$
mặt phẳng phân giác qua $A$ và có VTPT
$\underset{n}{\rightarrow}=\frac{\underset{n_1}{\rightarrow}}{|n_1|}+ -\frac{\underset{n_2}{\rightarrow}}{|n_2|}$
mình giải thích chỗ VTPT nhé
bạn lấy vectơ chia độ dài ra được véctơ băng nhau bằng 1
giông như bài hình toạ độ tổng hợp n là đường chéo của 2 vectơ đơn vị là 2 cạnh của hình thoi

Với bài toán này mình có biết 2 cáh giải
Cách 1 rút cho y=0 rú m theo x sử dụng đạo hàm
Cách 2 :
Xét $y'=3x^{2}-6x+m+2$
ta có $\Delta'=3-3m$
Điều kiện $(C_m)$ có 3 giao điểm với $Ox$ tai 3 điểm có hoành độ dương là đồ thị hàm số có 2 cực trị có tung độ trái dấu
ĐK có hai cự trị $y'=0  (*)$ có 2 nghiêm phân biệt => $m<1$
Gọi $x_1,x_2$ là nghiệm của $(*)$
Theo viet ta có $x_1+x_2=1             x_1.x_2=(m+2)/3$
ta có $3y(x_1)=x_1(3x_1^{2}-6x_1+m+2)-3x_1^{2}+6x_1-2m-2+2x_1(m-1)-5m+2=2x_1(m-1)-5m+2$
   $3y(x_2)=2x_2(m-1)-5m+2$
ycbt$\Leftrightarrow y(x_1).y(x_2)<0$ và  $y(0)<0$    
bạn nhân ra rồi thay viet vào rút ra đk của m
chỉ cần nhân ra cẩn thận và có kĩ năng là được

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

$y=x^{3}+mx^{2}+7x+3\rightarrow y'=3x^{2}+2mx+7$
Điều kiện $(C_m)$ có cực trị $y'=0$ có 2 nghiệm phân biệt $\Delta'=m^{2}-21>0\Leftrightarrow m^{2}>21$
Hai điểm cực trị thoả mãn 
$\begin{cases}3x^{2}+mx+7=0 \\ 3y=x^{2}(3x^{2}+mx+7)+2mx^{2}+14x+9 \end{cases}$
$\Rightarrow 3y+(2m^{2}/3-14)+14m/3-9=0$ đây chính là pt đường thẳng qua hai hai cực trị

$\int\limits_{0}^{\pi/6}e^{4sinx.sin(\pi/3-x).sin(\pi/3+x)}.sin12x.dx$

Xét phương trình hoành độ giao điểm của $(Cm)$ và $Ox$  pt$(*)$
Đặt $t=x^{2}$                $(*)$ theo $t$ có dạng  $t^{2}-2(m+1)t+2m+1=0  (**)$
                                                                $\Leftrightarrow (t-1)(t-2m-1)=0$
Điều kiện tồn tại $A,B,C,D   (*)$ có 4 nghiệm phân biệt   $(**)$ có 2 nghiệm dương phân biệt $\Rightarrow m>-1/2$
Xét $2m+1<1\Rightarrow A(-1;0)   C(\sqrt{2m+1};0)$
Ta có  $S_{\Delta ACK}=1/2d(K;Ox).AC=4\Leftrightarrow m=4 $  TM
Xét $2m+1>1\Rightarrow A(-\sqrt{2m+1};0)  C(1;0) $  tt  m=4
Vậy $m=4$ thoả đề

Bạn hãy tham khảo cách sau -có thể tính toán có sự sai sót nhưng m nghĩ hướng làm sau là đúng :)

Xét $I_1=\int\limits_{2}^{1}\frac{\sqrt{x^{2}-1}} {x} dx$
Đặt $\sqrt{x^{2}-1}=t\Rightarrow t^{2}=x^{2}-1\Rightarrow tdt=xdx$
Đổi cận   $x             2         1$
               
               $t         \sqrt{3}        0$
$I_1=\int\limits_{\sqrt{3}}^{0}\frac{t.t.dt}{(t^{2}+1)}=\int\limits_{\sqrt{3}}^{0}(1-\frac{1}{t^{2}+1})dt$
Xét $I_3=\int\limits_{\sqrt{3}}^{0}\frac{1}{t+t^{2}}$
Đặt $t=tan\alpha$       Với  $\alpha\in \left ( -\frac{\pi}{2};\frac{\pi}{2}\right )$
$\Rightarrow dt=(1+cos\alpha^{2})d\alpha$
Đổi cận       $t                  \sqrt{3}           0 $
                   $\alpha                 \pi/3            0$
$\Rightarrow I_3=\int\limits_{\pi/3}^{0}d\alpha$
$\Rightarrow  I_1=-\sqrt{3}+\pi/3$
Xét $I_2=\int\limits_{2}^{1}\frac{dx}{x^{2}\sqrt{1+1/x}} =   -  \int\limits_{2}^{1}\frac{d(1/x+1)}{\sqrt{1+1/x}}=\sqrt{6}-2\sqrt{2}$
Vậy  $I=I_1+I_2$

$A(4/5;7/5)  d_1: x-2y-1=0   d_2: x+3y-1=0$
Gọi $A_1$ đối xứng với $A$ qua $d_1  \rightarrow A1 \in BC$
       $A_2$ đối xứng với $A$ qua $d_2  \rightarrow A_2\in BC$
$AA_1 :2x+y-3=0   H1(7/5;1/5)=d_1\cap AA_1\rightarrow A_1(2;-1)$
$AA_2:3x-y-1=0  H_2(2/5;1/5)=d_2\cap AA_2\rightarrow A_2(0;-1)$
Vậy $BC: y=-1$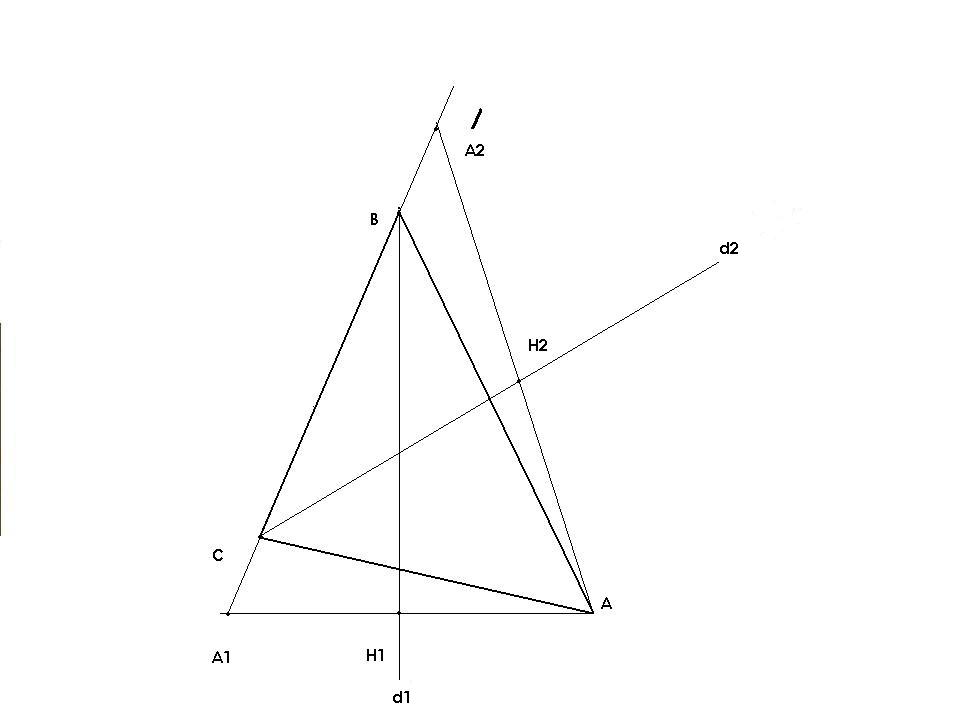